Реклама
Восьмеричний перехід
Опис роботи: Дана розробка призначена для вчителів інформатики та учнів старшої школи. У ній розглядаються деякі способи вирішення завдань на переклад чисел з однієї системи числення в іншу. Один із способів вирішення завдань - це комбінація кількох переказів. Наприклад, це може бути такий варіант: переклад з десяткової системи числення у вісімкову систему числення, а потім переклад з вісімковій системі числення в двійкову. У всіх комбінаціях перекладів бажаний перехід до вісімковій системі числення.
Завдання 1.
Уявити десяткове число 607 в двійковій системі числення.
Для переведення числа 607 в двійкову систему числення використовується спосіб, описаний у підручниках інформатики. Він полягає в діленні на 2 самого числа з отриманням частки і залишку, потім в розподілі всіх виходять приватних також з отриманням залишків до тих пір, поки останнє приватне не виявиться рівним 1. Цифрами двійкового числа стають остання одиниця, отримана як приватне, і залишки від поділок, виписані у порядку, зворотному їх отримання.
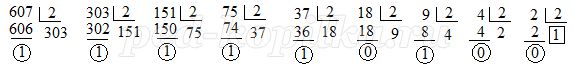Рис. 1
Це число 1001011111. Як видно з малюнка, тут досить багато поділок. Набагато швидше такий спосіб. Спочатку перевести число у вісімкову систему числення, а потім у двійкову.
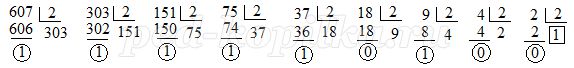Рис. 2
У вісімковій системі числення це буде число 1137. Замінюючи кожну цифру восьмеричного числа трьома двійковими цифрами 001 001 011 111 згідно таблиці 1, і відкидаючи два лівих нуля, як незначущі, отримаємо 10011111.
Табл. 1
Безсумнівно, що таку табличку необхідно пам'ятати, або відтворювати на досить простому алгоритму на папері.
Третій спосіб полягає в розкладанні числа 607 на суму ступенів двійки з коефіцієнтами при ступенях, рівними або 1, або 0. Для цього потрібно вміти відтворювати табличку ступенів двійки на папері або зберігати її в розумі. Максимальна ступінь двійки, яка є в числі 607 - це число 512 і вона повинна бути в сумі з коефіцієнтом 1. Далі запишемо в порядку убування ступеня двійки 256, 128, 64, 32, 16, 8, 4, 2, 1. Віднімаючи з 607 число 512, отримаємо 95. Значить, ступеня 256 128 можуть бути присутніми в сумі тільки з коефіцієнтом, рівним 0, а ступінь двійки - число 64 з коефіцієнтом, рівним 1. Далі, віднімаючи з 95 число 64, отримаємо 31, звідки випливає, що ступінь двійки - число 32 може бути присутнім в сумі тільки з коефіцієнтом 0 і т.д. Таким чином, 607 = 1*512 + 0*256 + 0*128 + 1*64 + 0*32 + 1*16 + 1*8 + 1*4 + 1*2 + 1*1. Коефіцієнти при степенях двійки, записані підряд, утворюють число 1001011111. Всі три способи привели до одного і того ж двійковому числу 1001011111.
Завдання 2.
Є 4 числа:
1) 101010111 - двійкове 2) 525 - вісімкове 3) 345 - десяткове 4) 15D - шістнадцяткове. Яке з них найменше?
Щоб порівняти числа, представлені у різних системах числення, треба отримати їх подання в одній системі числення. Краще всього вибрати для цього вісімкову систему числення. Для двійкового подання числа 101010111 скористаємося таблицею 1. Починаючи з молодшого розряду, розіб'ємо число на групи по три розряду і кожну групу замінимо на одну вісімкову цифру. Отримаємо вісімкове число 527. Тепер порівняємо це число з вісімковим числом 525 з другого варіанта відповіді. Найменше з них - число 525. Щоб уявити десяткове число 345 в вісімковій системі числення, скористаємося діленням на 8. В результаті першого поділу отримаємо перший залишок, рівний 1, і приватна, рівне 43. При поділі 43 на 8 отримаємо другий залишок, рівний 3 і приватне, рівну 5. Отже, десяткове число 345 в вісімковій системі числення - це число 531. З усіх трьох вісімкових чисел найменше - 525. Залишилося порівняти його з шістнадцятковим числом 15D. Для цього переведемо число 15D у вісімкову систему числення наступним чином: спочатку в двійкову систему числення за допомогою таблиці 2, замінюючи кожну цифру числа чотирма бітами.
Табл. 2
Це буде двійкова послідовність 0001 0101 1101. Потім, відкидаючи три крайніх лівих нуля (вони незначні) і розбиваючи двійкове число 101011101 на трійки 101 011 101, замінимо кожну трійку з допомогою таблиці 1 однією вісімковій цифрою, отримаємо вісімкове число 535. З двох вісімкових чисел 535 і 525 найменше число - 525. Таким чином, в якості відповіді задачі виберемо другий варіант відповіді.
Завдання 3
Дано: вісімкове число a = 233 і шістнадцяткове число b = 9E. Яке з чотирьох двійкових чисел не належить проміжку [a;b]?
1) 10011111 2) 10011101 3) 10011100 4) 10011011
Працюючи з таблицею 1, переведемо двійкові числа в вісімкову систему числення: 1)237 2)234 3)236 4)233. Складемо їх у порядку зростання: 233, 234, 236, 237. Оскільки мова в задачі йде тільки про одному числі, не належить проміжку [a;b], то, швидше за все, це буде число 237. Щоб переконатися в цьому, переведемо шістнадцяткове число b = 9E у вісімкову систему числення. Для цього переведемо його спочатку в двійкову систему числення, використовуючи таблицю 2. Це буде число 10011110. Потім отримане двійкове число розіб'ємо на групи по три розряду 10 011 110. Кожну групу з таблиці 1 замінимо однієї вісімковій цифрою. Отримаємо вісімкове число 236. Дійсно тільки вісімкове число 237 не належить проміжку [a;b] і відповіддю завдання буде перший варіант двійкового числа з чотирьох, запропонованих у завданні.
В даній задачі можливі й інші способи вирішення, наприклад, переклад чисел a і b в двійкову систему числення, а потім їх порівняння з тими, які є у відповіді. Однак зручніше порівняння більш коротких чисел. Можна було перевести всі числа задачі в десяткову систему числення, але в цьому випадку сам переклад чисел зажадає виконання досить великої кількості обчислень.
Восьмеричний перехід
У завданнях ЄДІ на роботу з числами в різних системах числення необхідно здійснювати переклад чисел з однієї системи числення в іншу. Способи перекладу відомі, вони описані в підручниках з інформатики. Однак іспит обмежує час на виконання завдань. Щоб виконати завдання не лише правильно, але й швидко, необхідно навчитися застосовувати в кожному конкретному завданні найбільш ефективні способи перекладу чисел.Завдання 1.
Уявити десяткове число 607 в двійковій системі числення.
Для переведення числа 607 в двійкову систему числення використовується спосіб, описаний у підручниках інформатики. Він полягає в діленні на 2 самого числа з отриманням частки і залишку, потім в розподілі всіх виходять приватних також з отриманням залишків до тих пір, поки останнє приватне не виявиться рівним 1. Цифрами двійкового числа стають остання одиниця, отримана як приватне, і залишки від поділок, виписані у порядку, зворотному їх отримання.
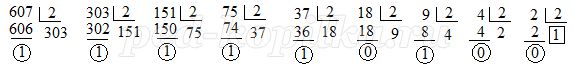
Це число 1001011111. Як видно з малюнка, тут досить багато поділок. Набагато швидше такий спосіб. Спочатку перевести число у вісімкову систему числення, а потім у двійкову.
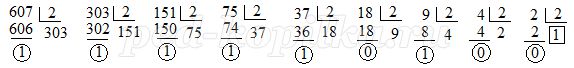
У вісімковій системі числення це буде число 1137. Замінюючи кожну цифру восьмеричного числа трьома двійковими цифрами 001 001 011 111 згідно таблиці 1, і відкидаючи два лівих нуля, як незначущі, отримаємо 10011111.
Безсумнівно, що таку табличку необхідно пам'ятати, або відтворювати на досить простому алгоритму на папері.
Третій спосіб полягає в розкладанні числа 607 на суму ступенів двійки з коефіцієнтами при ступенях, рівними або 1, або 0. Для цього потрібно вміти відтворювати табличку ступенів двійки на папері або зберігати її в розумі. Максимальна ступінь двійки, яка є в числі 607 - це число 512 і вона повинна бути в сумі з коефіцієнтом 1. Далі запишемо в порядку убування ступеня двійки 256, 128, 64, 32, 16, 8, 4, 2, 1. Віднімаючи з 607 число 512, отримаємо 95. Значить, ступеня 256 128 можуть бути присутніми в сумі тільки з коефіцієнтом, рівним 0, а ступінь двійки - число 64 з коефіцієнтом, рівним 1. Далі, віднімаючи з 95 число 64, отримаємо 31, звідки випливає, що ступінь двійки - число 32 може бути присутнім в сумі тільки з коефіцієнтом 0 і т.д. Таким чином, 607 = 1*512 + 0*256 + 0*128 + 1*64 + 0*32 + 1*16 + 1*8 + 1*4 + 1*2 + 1*1. Коефіцієнти при степенях двійки, записані підряд, утворюють число 1001011111. Всі три способи привели до одного і того ж двійковому числу 1001011111.
Завдання 2.
Є 4 числа:
1) 101010111 - двійкове 2) 525 - вісімкове 3) 345 - десяткове 4) 15D - шістнадцяткове. Яке з них найменше?
Щоб порівняти числа, представлені у різних системах числення, треба отримати їх подання в одній системі числення. Краще всього вибрати для цього вісімкову систему числення. Для двійкового подання числа 101010111 скористаємося таблицею 1. Починаючи з молодшого розряду, розіб'ємо число на групи по три розряду і кожну групу замінимо на одну вісімкову цифру. Отримаємо вісімкове число 527. Тепер порівняємо це число з вісімковим числом 525 з другого варіанта відповіді. Найменше з них - число 525. Щоб уявити десяткове число 345 в вісімковій системі числення, скористаємося діленням на 8. В результаті першого поділу отримаємо перший залишок, рівний 1, і приватна, рівне 43. При поділі 43 на 8 отримаємо другий залишок, рівний 3 і приватне, рівну 5. Отже, десяткове число 345 в вісімковій системі числення - це число 531. З усіх трьох вісімкових чисел найменше - 525. Залишилося порівняти його з шістнадцятковим числом 15D. Для цього переведемо число 15D у вісімкову систему числення наступним чином: спочатку в двійкову систему числення за допомогою таблиці 2, замінюючи кожну цифру числа чотирма бітами.
Це буде двійкова послідовність 0001 0101 1101. Потім, відкидаючи три крайніх лівих нуля (вони незначні) і розбиваючи двійкове число 101011101 на трійки 101 011 101, замінимо кожну трійку з допомогою таблиці 1 однією вісімковій цифрою, отримаємо вісімкове число 535. З двох вісімкових чисел 535 і 525 найменше число - 525. Таким чином, в якості відповіді задачі виберемо другий варіант відповіді.
Завдання 3
Дано: вісімкове число a = 233 і шістнадцяткове число b = 9E. Яке з чотирьох двійкових чисел не належить проміжку [a;b]?
1) 10011111 2) 10011101 3) 10011100 4) 10011011
Працюючи з таблицею 1, переведемо двійкові числа в вісімкову систему числення: 1)237 2)234 3)236 4)233. Складемо їх у порядку зростання: 233, 234, 236, 237. Оскільки мова в задачі йде тільки про одному числі, не належить проміжку [a;b], то, швидше за все, це буде число 237. Щоб переконатися в цьому, переведемо шістнадцяткове число b = 9E у вісімкову систему числення. Для цього переведемо його спочатку в двійкову систему числення, використовуючи таблицю 2. Це буде число 10011110. Потім отримане двійкове число розіб'ємо на групи по три розряду 10 011 110. Кожну групу з таблиці 1 замінимо однієї вісімковій цифрою. Отримаємо вісімкове число 236. Дійсно тільки вісімкове число 237 не належить проміжку [a;b] і відповіддю завдання буде перший варіант двійкового числа з чотирьох, запропонованих у завданні.
В даній задачі можливі й інші способи вирішення, наприклад, переклад чисел a і b в двійкову систему числення, а потім їх порівняння з тими, які є у відповіді. Однак зручніше порівняння більш коротких чисел. Можна було перевести всі числа задачі в десяткову систему числення, але в цьому випадку сам переклад чисел зажадає виконання досить великої кількості обчислень.