Конспект уроку з геометрії в 7 класі з теми «Співвідношення між сторонами і кутами трикутника»

Автор: Малкова Світлана Василівна, вчитель математики ЗОШ №40», р. Саранськ
Опис матеріалу: Пропоную вам конспект уроку в 7 класі з теми «Співвідношення між сторонами і кутами трикутника. Розглядається одна з найважливіших теорем геометрії - теорема про суму кутів трикутника. Теорема дозволяє отримати важливі слідства - властивість зовнішнього кута трикутника, деякі властивості прямокутних трикутників. Потім розглядаються співвідношення між сторонами і кутами трикутника, нерівність трикутника.
Даний матеріал розрахований для вчителів середньої школи.
Мета:
1.повторити та узагальнити вивчений матеріал;
2.Формировать уміння міркувати;
3.Развивать логічне мислення учнів;
4.Проверить рівень засвоєння теми.
Тип уроку:узагальнення та систематизація знань.
Обладнання:комп'ютер,проектор,екран.
План уроку.
1.Организационный момент.
2.Теоретический опитування.
3.Устная робота.
4.Геометрический диктант.
5.Готовимся до ДПА.
6.Решение завдань.
7.Исторические відомості.
8.Тестовая робота.
9.Домашнее завдання.
10.Итог уроку.Хід уроку
1.Организационный момент.
Діти, сьогоднішній урок хочу почати словами відомого математика А. Маркушевича: «Через математичні знання, отримані в школі, лежить широка дорога до величезних, майже неозорими областях праці та відкриттів».
Девіз нашого уроку «Думаємо, думаємо,працюємо і допомагаємо один одному».
Тему уроку ви дізнаєтеся,якщо виконайте наступне завдання:розв'яжіть анаграми (у словах змінено порядок букв). Які слова зашифровані?
1.олгу (кут)
2.тосроан (сторона)
3.кельногутри (трикутник)
4.сотоешонине (співвідношення)
Яка тема об'єднує ці слова? (Співвідношення між сторонами і кутами трикутника).
Сьогодні ми згадаємо і узагальнимо ті знання, які ви отримали на попередніх уроках. Отже, відкрийте зошити і запишіть тему уроку: «Співвідношення між сторонами і кутами трикутника».
2.Теоретический опитування.
1)Сформулюйте теорему про суму кутів трикутника.
2)Який кут називається зовнішнім кутом трикутника?
3)Чому дорівнює зовнішній кут трикутника?
4)Який трикутник називається гострокутним?
5)Який трикутник називається тупоугольным?
6)Який трикутник називається прямокутним?
7)Як називаються сторони прямокутного трикутника?
8)Сформулюйте теорему про співвідношення між сторонами і кутами трикутника.
9)Сформулюйте нерівність трикутника.
10)Сформулюйте властивості прямокутних трикутників.
3.Устная робота.
- Знайти невідомі кути трикутника.
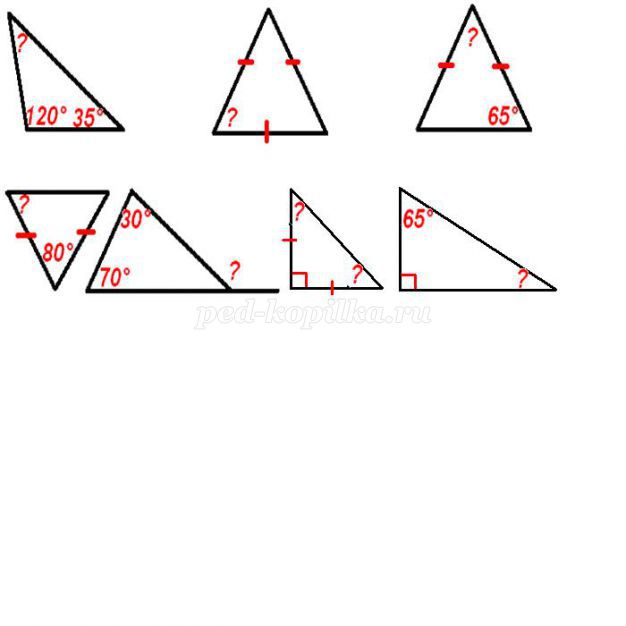
- Яка сторона у трикутнику найбільша?
A=35°, В=67°,=78°.
A=80°, В=68°.
- Який кут у трикутнику найбільший?
ВС=5 см, АС=6 см, АВ=7см.
ВС=10 см, АС=8 см, АВ=6см.
- Чи існує трикутник зі сторонами?
2см, 4см, 6 див.
4см, 5см, 6 див.
4.Геометрический диктант.
Закінчите пропозицію.
1.У трикутнику сума кутів дорівнює...
2.Внешний кут трикутника дорівнює...
3.Каждая сторона трикутника ... суми двох інших сторін.
4.У трикутнику проти більшої сторони лежить ...
5.В трикутнику проти меншого кута лежить ...
6.якщо в трикутнику два кути рівні, то...
7.Сумма двох сторін трикутника ...
8.Сторона прямокутного трикутника, що лежить проти прямого кута, називається...
9.Длина гіпотенузи в прямокутному трикутнику...
10.Во всякому трикутнику проти рівних сторін лежать...
Відповіді:
1) 180°;
2) суми двох кутів трикутника, не суміжних з ним;
3) менше;
4) більший кут;
5) менша сторона;
6) трикутник рівнобедрений;
7) більше третьої сторони;
8) гіпотенузою;
9) більше катета
10) рівні кути
5.Готовимся до ДПА.
Завдання 1. У трикутнику ABC AD - бісектриса, З=103°, CAD=4°.
Знайдіть Ст.
Рішення.

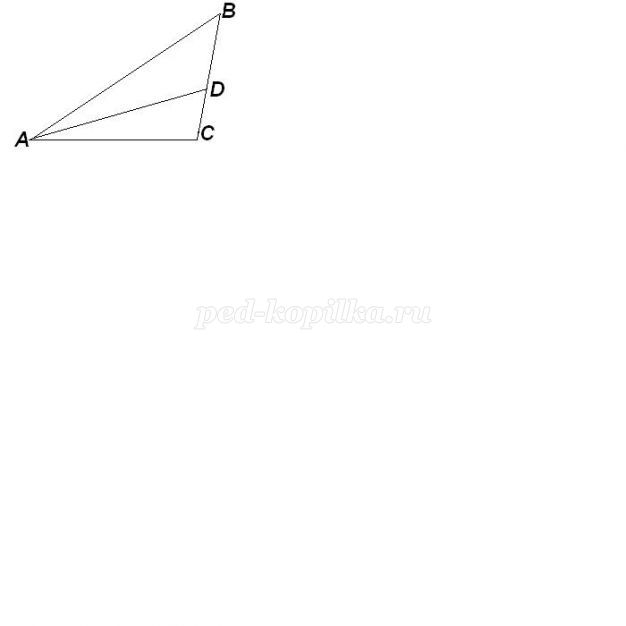
Так як AD - бісектриса А, то А=8°, тоді В=180°-(103°+8°)=69°.
Завдання 2. Один з гострих кутів прямокутного трикутника в два рази більше іншого. Знайти менший гострий кут.
Рішення.

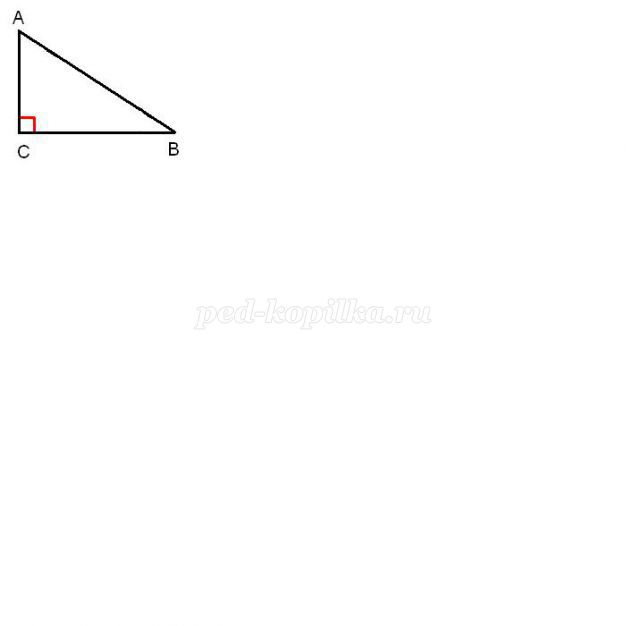
Сума гострих кутів прямокутного трикутника дорівнює 90°, 90° : 3=30°.
Відповідь: 30°.
6. Рішення завдань.
Завдання 1. Один з кутів прямокутного трикутника дорівнює 60°, сума гіпотенузи і меншого катета дорівнює 42 див. Знайти гіпотенузу.
Рішення.

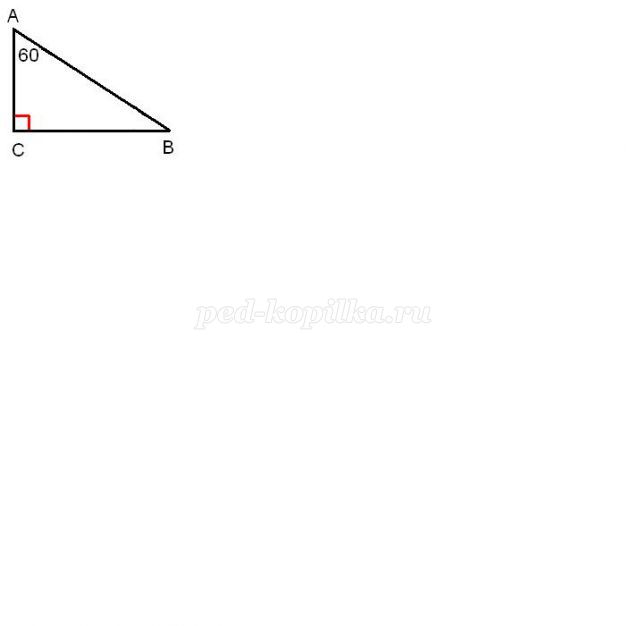
В=30° => АВ+АС=42; АВ+ АВ=42; 1 АВ=42; АВ=42 =28 див.
Відповідь: 28 див.
Завдання 2. У равнобедренном трикутнику один з кутів 120°, а основа дорівнює 4 див. знайти висоту, проведену до бічної сторони.
Рішення.

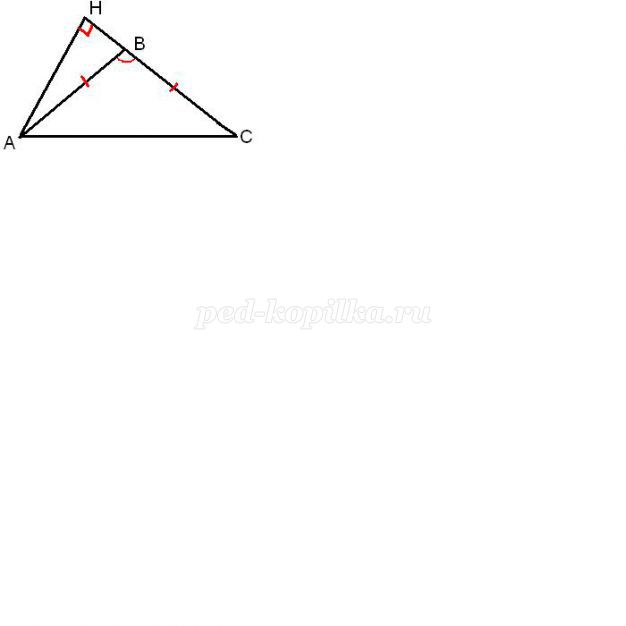
1) У=120° - при вершині рівнобедреного трикутника, тоді А= С= 30°.
2) АН - висота ∆ АВС, тоді ∆ АНС - прямокутний, в ньому З= 30°, значить АН= АС=2 див.
Відповідь: 2 див.
Додатково:
Завдання. Знайти кути прямокутного трикутника, якщо кут між бісектрисою і висотою, проведеними з вершини прямого кута, дорівнює 15°.
Рішення.

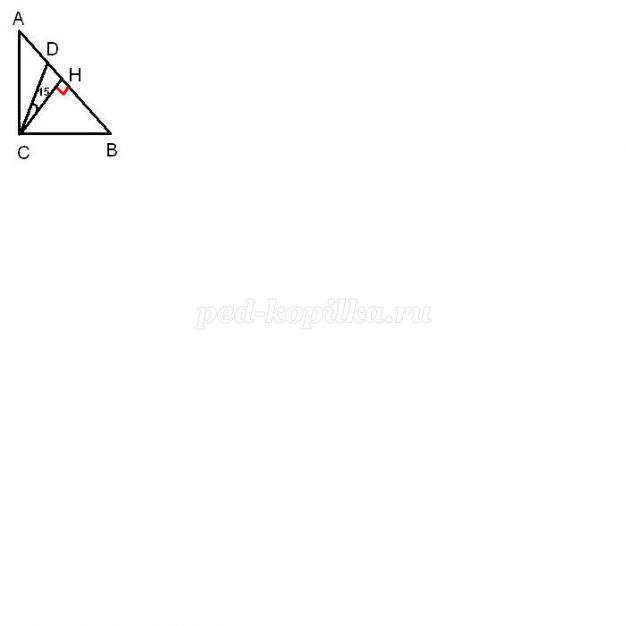
CD - бісектриса, СН - висота.
1) DCH=15° (по умові). DCА=45°, тоді НСА=45°-15°=30°.
2) трикутник НСА - прямокутний, НСА=30°, тоді САН=60°.
3) трикутник АВС - прямокутний, З=90°, А=60°, тоді В=30°.
Відповідь: 30°; 60°; 90°.
7.Исторические відомості.
Значних успіхів в геометрії змогли домогтися єгиптяни. Відомо, що в середині першого тисячоліття до н.е. для побудови прямого кута єгиптяни використовували мотузку, розділену вузлами на 12 рівних частин. Кінці мотузки пов'язували і натягували її на три кілочка у вигляді трикутника зі сторонами 3, 4, 5. Кут між сторонами, рівними 3 і 4, опинявся прямим.
Вже піфагорійцям було відоме, що є тільки три види правильних многокутників, якими можна повністю замостити площину без пробілів і перекриттів, - трикутник, квадрат і шестикутник. У кожному з цих замощений будь-які два багатокутника або мають спільну сторону, або загальну вершину. Замощення площині багатокутниками, що задовольняють цій вимозі, називають паркетом. Використовують у будівництві, при оздоблювальних роботах в архітектурі.
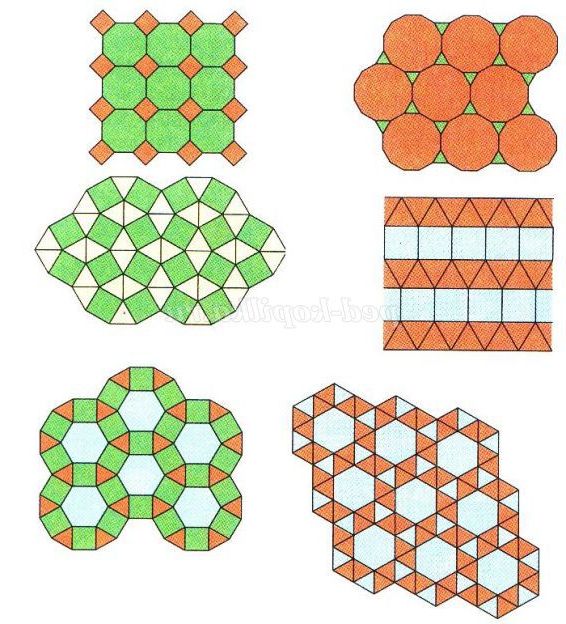
8.Тестовая робота.
Варіант перший.
1) Серед трикутників ABC, EFO, KLM знайти гострокутний.
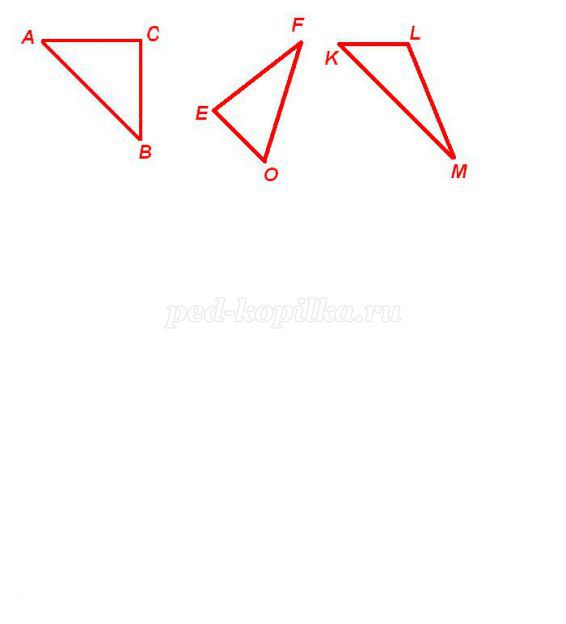
а) трикутник KLM
б) трикутник EFO
в) трикутник ABC
2) Знайти невідомий кут трикутника.
а) 59°
б) 39°
в) 49°
3) Знайти невідомий катет АС, якщо АВ=48 див., В=30°.
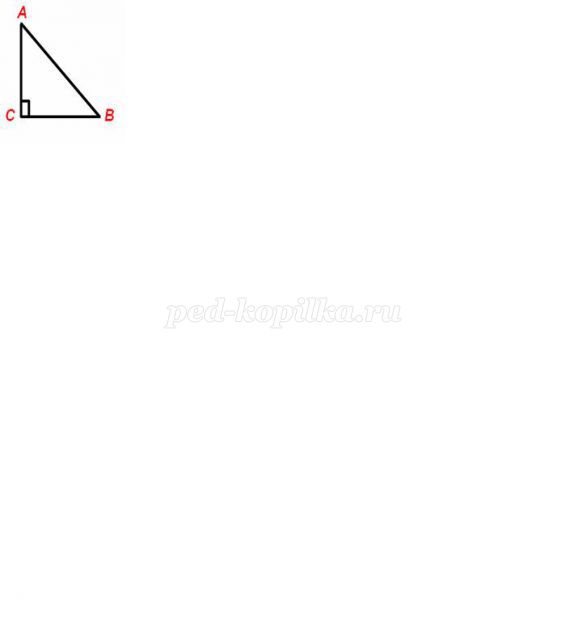
а) 48 див.
б) 30 см.
в) 24 див.
4) Знайти невідомий кут трикутника.
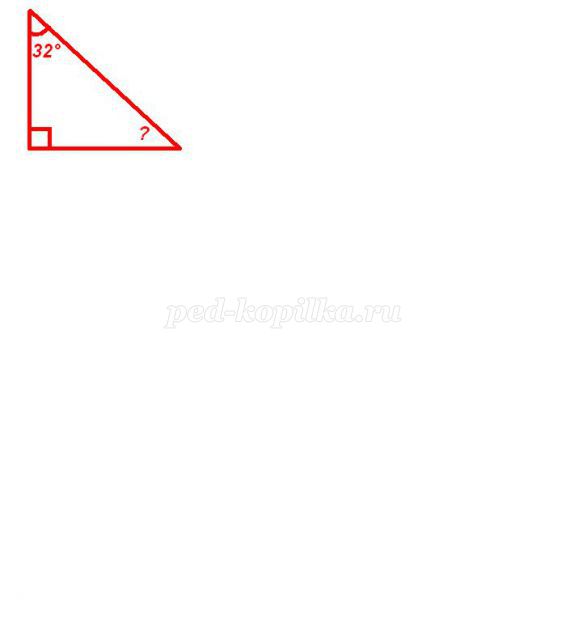
а) 62°
б) 58°
в) 48°
5) Знайти невідомий А, якщо АВ=15 см, ВС=7,5 див.
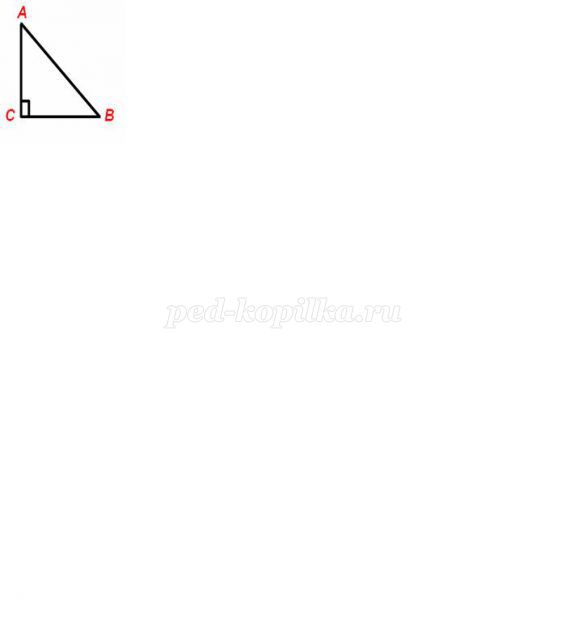
а) 45°
б) 30°
в) 60°
6) Знайти невідомі кути трикутника, якщо А: В: С=4:6:8.
а) А=40°=60° С=80°
б) А=80°=60°=40°
в) А=60°=40° С=80°
7) Знайти невідомі кути трикутника.
а) 1=53° 2=63° 3=54°
б) 1=53° 2=63° 3=64°
в) 1=63° 2=53° 3=64°
Другий варіант.
1) Серед трикутників ABC, EFO, KLM знайти тупокутний.
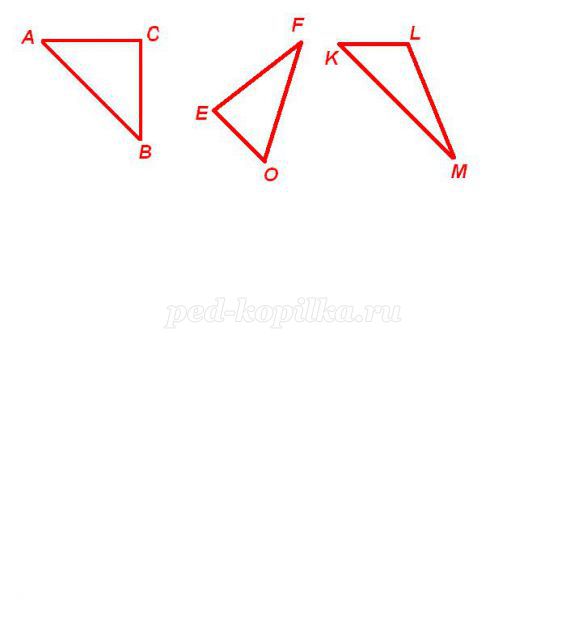
а) трикутник KLM
б) трикутник EFO
в) трикутник ABC
2) Знайти невідомий кут трикутника.
а) 32°
б) 42°
в) 38°
3) Знайти невідомий катет, якщо АВ=36 см, В=30°.
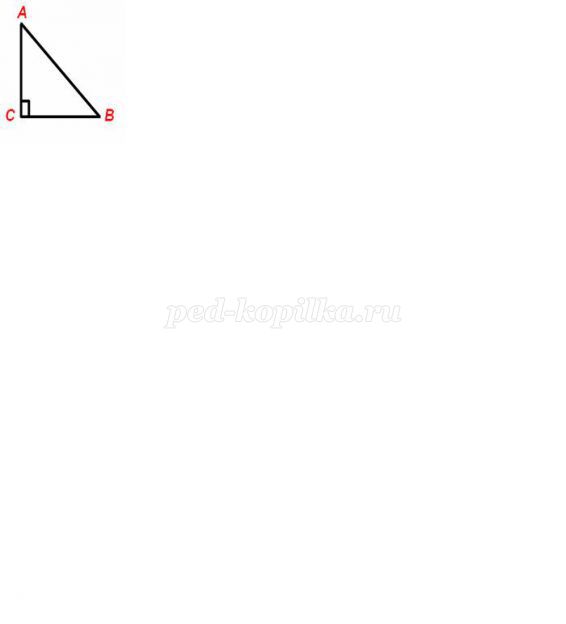
а) 36 див.
б) 40 див.
в) 18 див.
4) Знайти невідомий кут трикутника.
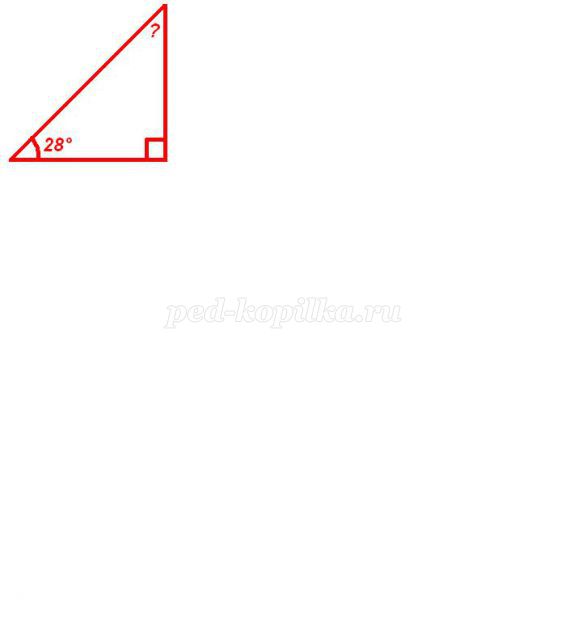
а) 52°
б) 62°
в) 72°
5) Знайти невідомий, якщо АВ=40 см, АС=20 див.
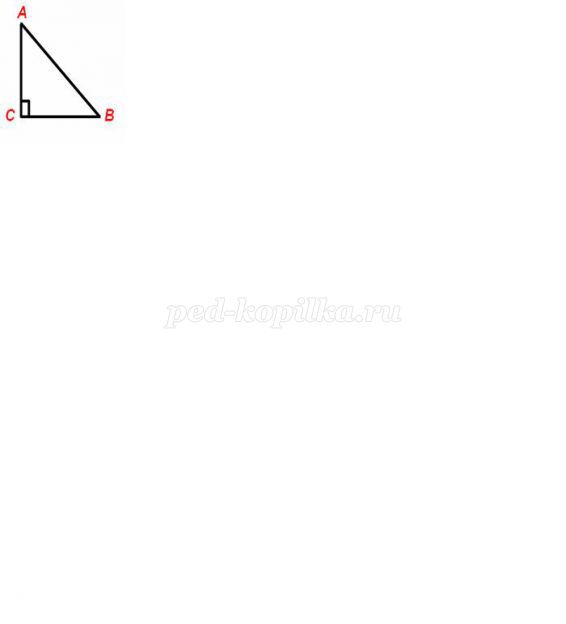
а) 45°
б) 60°
в) 30°
6) Знайти невідомі кути трикутника, якщо А: В: С=4:5:9.
а) А=50°=40° С=90°
б) А=40°=50° С=90°
в) А=90°=50° С=40°
7) Знайти невідомі кути трикутника.
а) 1=48° 2=57° 3=75°
б) 1=58° 2=48° 3=65°
в) 1=57° 2=48° 3=75°
Відповіді:

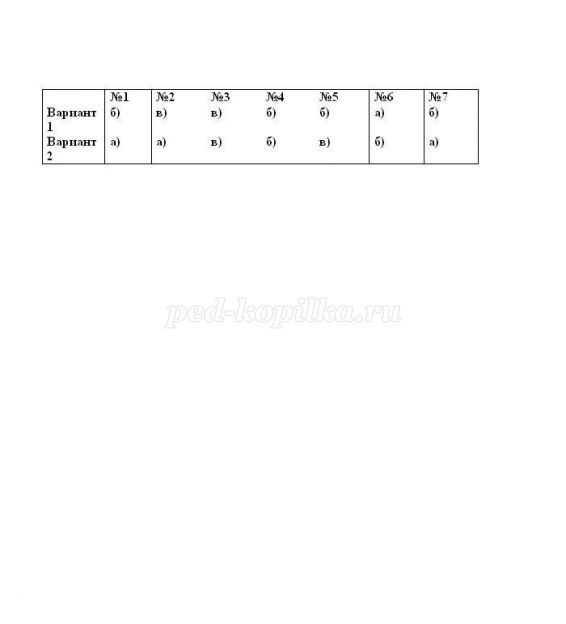
9.Домашнее завдання: повторити главу 4, №296.
Скласти кросворд або малюнок із трикутників.
10.Итог уроку. Виставлення оцінок.
Рефлексія:
1. Які цілі до уроку ставили?
2. Чи досягли ми їх?
3. Як Ви оцінюєте свою роботу на уроці?
Спасибі за урок.